TEORIA DE CONJUNTOS

 1-.Concepto de conjunto. Se denomina conjunto a la agrupación de entes o elementos, que poseen una o varias características en común. Es un concepto intuitivo empleado en matemática, que elaboró la teoría de conjuntos.

Para otros usos de este término, véase Conjunto (desambiguación).

Los diversos polígonos en la imagenconstituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos —los polígonos regulares en la imagen— es otro conjunto, en particular, un subconjunto del primero.

En matemáticas, un conjunto es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

Ejemplo: el conjunto de los colores del arcoíris es:

AI = {Ros es:

P = {2, 3, 5, 7, 11, 13, ...}

El término conjunto es bastante primitivo y fundamental en toda la estructura matemática. Generalmente, esta palabra se acepta en matemáticas como un término indefinido, tal como en geometría que toma, entre otros, los términos punto, línea, plano, que sin definición pero si de manera intuitiva. Similarmente sucede con el término elemento.
La teoría de conjuntos es una parte de las matemáticas que tiene un objeto de estudio propio; con métodos propios, con ciertas relaciones con otras teorías matemáticas, en particular, con todas las teorías matemáticas tradicionales y a partir de sus principios se mantiene la existencia, estructura y relaciones mutuas entre ellos. Es decir, que el resto de la matemática puede expresarse en términos de conjuntos.
Georg Cantor (1845–1918) matemático, físico y filósofo alemán de origen ruso. Se doctoró en 1867 y empezó a trabajar como profesor adjunto en la Universidad de Halle. En 1874 publicó su primer trabajo sobre teoría de conjuntos. Es considerado como el padre de “la teoría de conjuntos”.
Cantor operó con conjuntos infinitos, transformando unos en otros mediante reglas precisas, los comparó respecto a su cardinalidad y mostró cómo asignar un número cardinal a cada conjunto. Entre sus primeros resultados encontró que dos conjuntos tienen la misma cardinalidad, si tienen correspondencia biunívoca entre ellos. Si dos conjuntos no tienen la misma cardinalidad, pero tienen correspondencia biunívoca con un subconjunto de otro, la cardinalidad del primero es menor que la del segundo.
Su mente luchó contra varias paradojas de la teoría de conjuntos, en otras la paradoja de Bertrand Russell, que parecían invalidar toda su teoría; es decir, la hacía inconsistente o contradictoria, en el sentido de que una cierta propiedad podría ser a la vez cierta y falsa.
A fines de mayo de 1884 Cantor tuvo su primer ataque registrado de depresión. Se recuperó después de unas cuantas semanas, pero aparecía menos confiado. En junio de 1917 ingresó una institución mental de Halle (ciudad del centro de Alemania) por última vez; de allí le escribía continuamente a su esposa pidiendo que le permitiera regresar a casa. Murió en un ataque cardiaco, el 6 de enero de 1918, cuando tenía 73 años de edad.

7.2 Concepto de conjunto

Se llama conjunto a toda agrupación, colección o reunión de individuos (cosas, animales, personas o números) bien definidos que cumplen una propiedad determinada. A los objetos del conjunto se denominan “elementos”.

Ejemplo 7.1: Los siguientes son algunos ejemplos de conjunto:
. El conjunto formado por los colores de la bandera de Colombia.

. La colección de letras de la palabra “murciélago”.

.El conjunto formado por los dígitos del número 345923238.

.La agrupación de números naturales menores que 10

.La agrupación de números primos entre 0 y 20.

7.3 Notación de conjuntos

Ejemplo 7.2: utilice la notación correcta para escribir los conjuntos dados en el ejemplo 7.1

A= El conjunto formado por los colores de la bandera de Colombia.

B= La colección de letras de la palabra “murciélago”

C= El conjunto formado por los dígitos del número 345923238

D= La agrupación de números naturales menores que 10

E= La agrupación de números primos entre 0 y 20

7.4 Determinación de conjuntos

La determinación de un conjunto corresponde a la manera como éste puede expresarse. Para determinar un conjunto se utilizan dos formas: determinación por extensión y la determinación por comprensión.

7.4.1 Determinación de conjuntos por extensión

Un conjunto se determina por extensión cuando se enumeran o se nombran los elementos del conjunto. Cuando el conjunto es finito se escriben entre llaves, separados por comas. Cuando el conjunto es infinito se escriben entre llaves algunos elementos y se ponen puntos suspensivos

Ejemplo 7.3: Determine por extensión los conjuntos del ejemplo 7.2

A={amarillo, azul, rojo}

B={m, u, r, c, i, e, l, a, g, o}

C={3,4,5,9,2,8}, no se repiten elementos

D={1, 2, 3, 4, 5, 6, 7, 8, 9}

E={1, 2, 3, 5, 7, 11, 13, 17, 19}

7.4.2 Determinación de conjuntos por comprensión

Un conjunto se determina por comprensión enunciando la propiedad o cualidad que distingue a los elementos. Para tal fin se utiliza lo siguiente:
{x/x cumple la propiedad},
que se lee: el conjunto de las x tal que x cumple la propiedad

Ejemplo 7.3: Determine por comprensión los conjuntos del ejemplo 7.2

A={x/ x es un color de la bandera de Colombia}

B={x/ x es una letra de la palabra “murciélago”}

C={ x/ x es un dígito del número 345923238}

D={ x/ x es un número natural menor que 10}

E={ x/ x es número primo entre 0 y 20}

7.5 Representación de conjuntos

Existen varias formas de representar los conjuntos: representación gráfica y representación en la computadora.

7.5.1 Representación gráfica de conjuntos

Los conjuntos se pueden representar gráficamente mediante diagramas de Venn y por diagramas de Caroll.
Diagramas de Venn (figura 7.1). Estos diagramas fueron descubiertos por el lógico y matemático británico John Venn (1834–1923). El sistema de representación que hoy conocemos fue desarrollado en julio de 1880 con la publicación titulada “De la representación mecánica y diagramática de proposiciones y razonamientos” en el Philosophical Magazine and Journal of Science, lo cual provocó cierto revuelo en el mundo de la lógica formal. Esta representación más conocida como “diagramas de Venn”, consisten en figuras geométricas planas y cerradas; dentro de cada figura se ponen los elementos que le corresponden. Estos diagramas serán los utilizados en el desarrollo de este texto.

Diagramas de Carroll (figura 7.2). Son bastante útiles para el estudio de las propiedades de los complementos de conjuntos. Consisten en líneas perpendiculares que se cortan (una horizontal y otra perpendicular) tal que un plano cartesiano; en la parte superior e inferior de la línea horizontal se ponen los elementos que cumplen una propiedad y de manera similar al lado izquierdo y derecho de la línea vertical. De tal manera se pueden realizar las operaciones entre conjuntos.

7.5.2 Representación de conjuntos en la computadora

Un conjunto se puede representar en la computadora como arreglo unidimensional de longitud n (n número de elementos de A) que en el argot de la computación se denomina “vector” y por lo tanto, se pueden realizar las operaciones que hacen con conjuntos: intersección (datos repetidos de los vectores, eliminando los repetidos), unión (poniendo los elementos de los vectores, pero eliminando los repetidos) y así sucesivamente con la diferencia y el complemento.
Este tema sen tratará al final de este capítulo. Se recomienda para su estudio recordar los conceptos acerca del manejo de arreglos en computación.

7.6 Relaciones de conjuntos

Las relaciones que se pueden dar entre conjuntos son: pertenencia, inclusión e igualdad.

7.6.1 Relación de pertenencia

El signo que representa la relación de pertenencia es E, que fue descubierto por el matemático y filósofo italiano, Giuseppe Peano (1858 –1932), quien es conocido por sus contribuciones a la Teoría de conjuntos.
En efecto, sea A un conjunto cualquiera y x un elemento, para indicar que x es elemento de A o simplemente que, x está en A se simboliza

verá en la sección 6.9; tampoco se da entre elementos. Por lo tanto, es incorrecto escribir x E x o A E A

7.6.2 Relación de Inclusión de conjuntos

Dados dos conjuntos A y B, esta relación se utiliza para indicar que el conjunto A es subconjunto del conjunto B, lo cual se escribe:

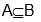
y se lee: A es subconjunto de B, A está incluido en B, A está contenido en B, B incluye a A.

Si A es un subconjunto de B y existen elementos de B que no están en A, entonces A es un subconjunto propio de B y se simboliza

7.6.3 Propiedades de la inclusión

Sus demostraciones son sencillas; basta con utilizar las propiedades las definiciones de inclusión y pertenencia, además, de las propiedades de cuantificadores. En efecto veamos, x E A Por hipótesis

Ejemplo 7.5: dados los conjuntos A={3,5,6,9,4}, B={3,4,7,9,6,5} y C={3,9,5,7,4,6,8,} ponga entre el paréntesis V o F si los siguientes enunciados son verdadero o falso, respectivamente y justifique el por qué de los falsos.

Según el ejemplo se puede observar que A es subconjunto propio de B y a la vez éste de C.

7.6.4 Relación de igualdad de conjuntos

La igualdad de dos conjuntos A y B denotada
A=B

se da cuando todos los elementos de A están en B y viceversa. Simbólicamente,

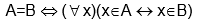
Esta equivalencia se conoce como axioma de extensionalidad. La igualdad de conjuntos intuitivamente dice: “dos conjuntos son iguales si y solo tienen los mismos elementos (no importa el orden)”. Tenga en cuenta que este concepto es diferente a decir: “dos conjuntos son iguales si y solo tienen la misma cantidad de elementos”.
Si algún elemento x de A no está en B o algún elemento x de B no está en A se dice que A es diferente de B y se simboliza

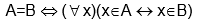
Ejemplo 7.6: dados los conjuntos
A={x/x es un número primo positivo menor que 8},

B={ x/x es un factor de 210}

¿A=B? Compruébelo.
A={2,3,5,7}

B={2,3,5,7}
Luego, los conjuntos son iguales

7.7 Clases de conjuntos

7.7.1 Conjunto finito

Es aquel conjunto cuya cantidad de elemento se puede contar; es decir, es aquel conjunto en que sus elementos se pueden nombrar o enumerar.
Ejemplo 7.9: A={x/x es un número entero mayor o igual que -3 y menor que 5}. Este conjunto está formado por 8 elementos. En efecto, A={-3, -2, -1, 0, 1, 2, 3,4}

7.7.2 Conjunto vacío

Existe un conjunto especial denominado “conjunto vacío” o “conjunto nulo” y algunos definen como un conjunto sin elementos. Este último concepto se presta para confusiones cuando se dice “conjunto sin elementos”; pues se sabe que un conjunto es una agrupación de objetos que cumplen una propiedad determinada.
Esta confusión se aclara defiendo el conjunto vacío como aquel en que ningún elemento cumple con la propiedad conocida como “regla de elegibilidad”.

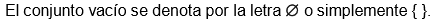
No es correcto decir, “un conjunto vacío”; debe decirse siempre “el conjunto vacío” porque este conjunto es único.

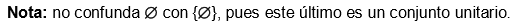
7.7.3 Propiedades del conjunto vacío

Ejemplo 7.10: los siguientes ejemplos ayudan a conceptualizar el conjunto vacío: